Hermitian form, inner product and symplectic form relationship
See before: complexification of a vector space.
(See at Calibre library the document: Complexification, complex structures, inner products, symplectic forms and linear differential equations, page 4)
To sum up, in a real vector space $V$ with a complex structure $J$, one real inner product determine a symplectic form and viceversa.
Moreover, an inner product $h$ defined in $V$ seen as a complex vector space (keep an eye: an Hermitian inner product) determine in $V$ an inner product $g$ (in the real sense) and a symplectic form $\omega$ in such a way that
$$ h\left(v_{1}, v_{2}\right)=g\left(v_{1}, v_{2}\right)-i \omega\left(v_{1}, v_{2}\right) $$If B is a bilinear form on $V$ then we say that $J$ preserves B if
$$ B(Ju,Jv)=B(u,v) $$for all $u, v \in V$.
An equivalent characterization is that $J$ is skew-adjoint with respect to B:
$$B(Ju,v)=-B(u,Jv)$$
If $g$ is an inner product on $V$ then $J$ preserves $g$ if and only if $J$ is an orthogonal transformation. Likewise, $J$ preserves a nondegenerate, skew-symmetric form $\omega$ if and only if J is a symplectic transformation (that is, if $\omega(Ju, Jv) = \omega(u, v)$). For symplectic forms $\omega$ there is usually an added restriction for compatibility between $J$ and $\omega$, namely
$$ \omega (u,Ju)>0$$
for all non-zero $u \in V$. If this condition is satisfied then $J$ is said to tame $\omega.$
Given a symplectic form $\omega$ and a linear complex structure $J$, one may define an associated symmetric bilinear form $g_J$ on $V_J$
$$ g_{J}(u,v)=\omega (u,Jv) $$Because a symplectic form is nondegenerate, so is the associated bilinear form. Moreover, the associated form is preserved by $J$ if and only if the symplectic form is, and if $\omega$ is tamed by $J$ then the associated form is positive definite. Thus in this case the associated form is a Hermitian form and $V_J$ is an inner product space.In handwritten notes:

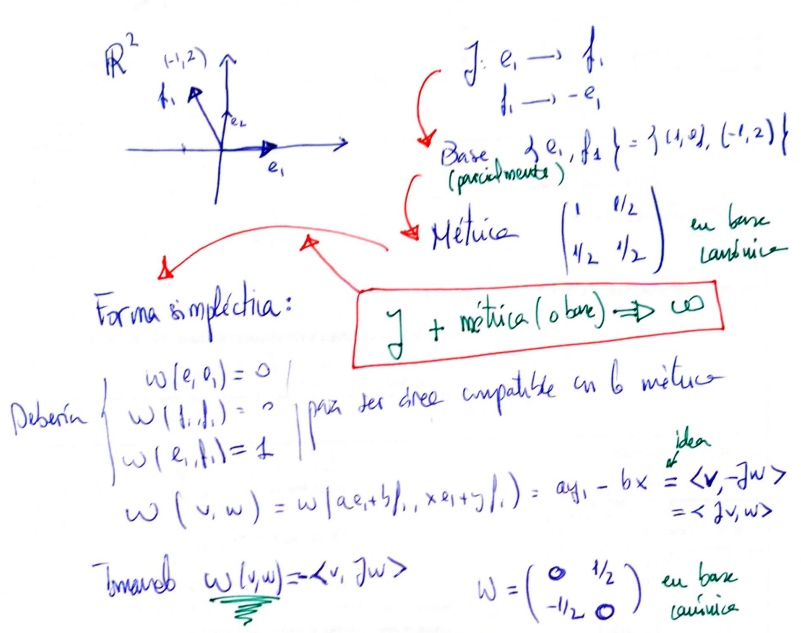

________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: